Какие фигуры ты знаешь? Квадрат, круг, треугольник. Этого вполне достаточно для повседневных задач. Но форм куда больше, чем ты можешь себе представить, и они порой настолько необычные, что кажется, будто их выдумали, просто чтобы потренироваться в фантазии.
1. Тор
Если говорить научным языком, тор, или, как его ещё называют, тороид, — это поверхность, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её. Звучит непонятно, и человеку, незнакомому с геометрией, вообще невозможно представить, что это такое.
А на самом деле всё просто, ведь тор ты видишь каждый день — это форма бублика, пончика, спасательного круга, шины колеса и всего похожего на них. Что касается природы, то и в ней встречаются такие фигуры. Например, форму тора имеют вихревые потоки, электромагнитные поля, траектории элементарных частиц.
Так что в следующий раз, когда тебя спросят, какую форму имеет пончик, можешь сказать, что это тор.
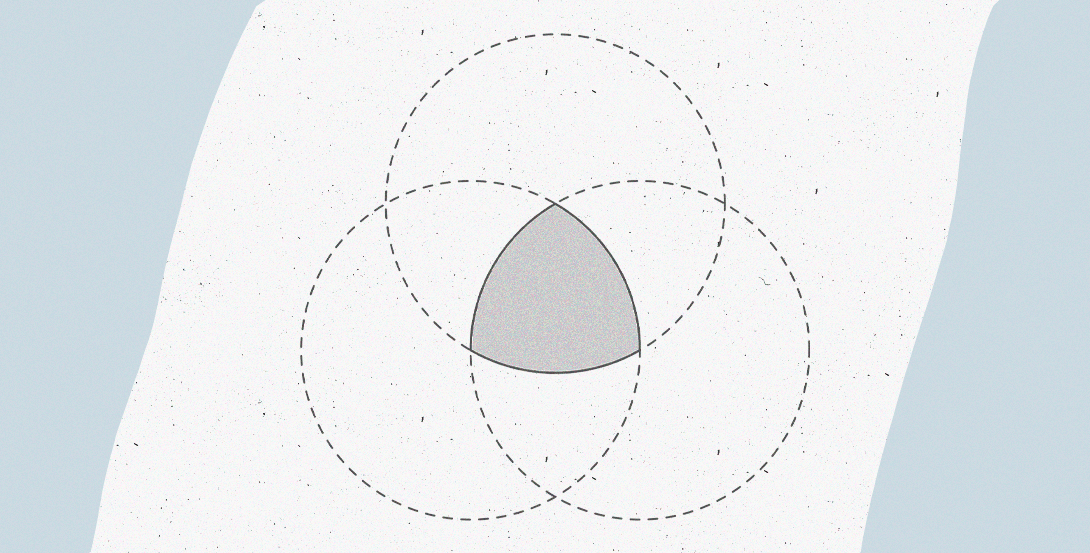
2. Треугольник Рёло
Треугольник Рёло — это область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Сам треугольник чем-то напоминает медиатор для гитары и имеет не прямые, а изогнутые грани.
Его ты тоже регулярно встречаешь в обычной жизни. Так, например, треугольник Рёло используют в сфере искусства для уже упомянутых струнных инструментов, а также при рисовании различных диаграмм, где несколько элементов по кругу, сочетаясь между собой, приводят к центральному ядру.
Кроме того, треугольник Рёло — это одна из первых изобретённых человеком форм, так как древние люди, изготавливая свои примитивные орудия труда из камня, нередко обтачивали их именно в такой форме, что позволяло использовать их с любой стороны.
3. Гиперболоид
Гиперболоид — это трёхмерная форма, которая напоминает песочные часы. Существуют однополостные и двухполостные гиперболоиды. Вторые ты можешь увидеть в тех знаменитых тарелках спутниковой связи, а также в телескопах, если интересуешься астрономией. Не путай гиперболоид с гиперболой — это разные вещи.
5 распространенных ошибок при изучении чего-то нового
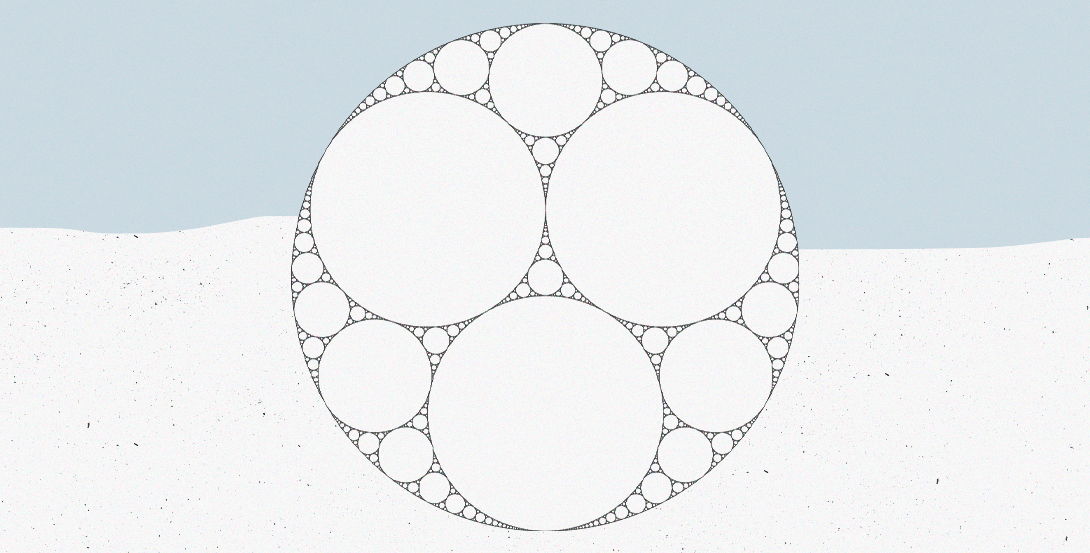
4. Аполлонийская прокладка, или аполлоническая сетка
Это очень сложная фигура, состоящая из одного большого круга с кругами меньшего размера, которые заполняют пространство внутри него.
Эта фигура редко где используется, и её можно было встретить в старых калейдоскопах, а также в искусстве. В художественных школах иногда ученики рисуют аполлонийские прокладки для отработки навыка рисования ровных кругов от руки.
5. Балбис
Думаешь, что буква Н — это просто буква? На самом деле это геометрическая форма, которую по-простому можно описать как одну первичную линию, которая завершается вторичной линией на одном конце и ещё одной — на другом. Завершающие линии располагаются под прямым углом к первичной, а его параллельные стороны могут быть бесконечно длинными.
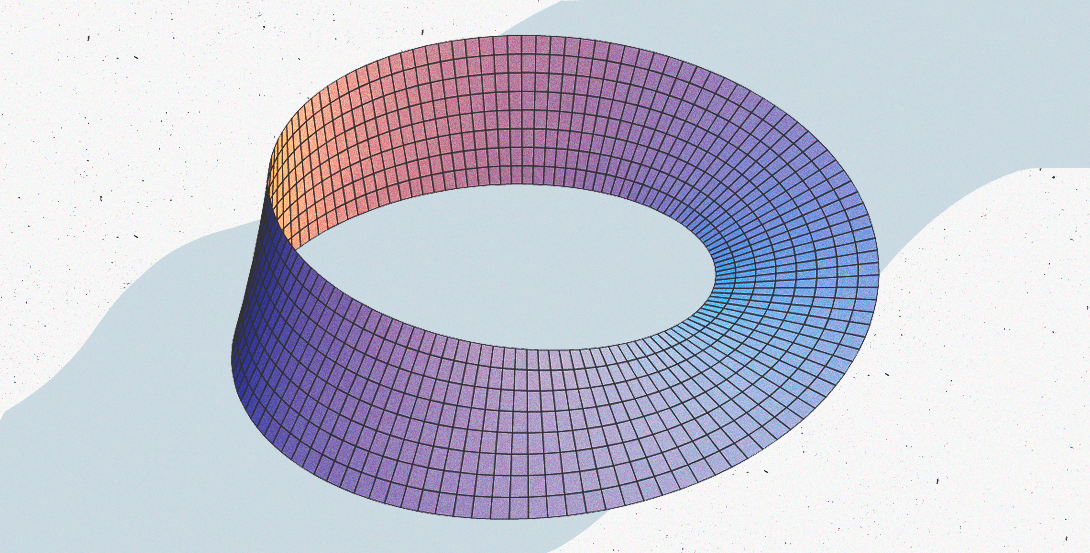
6. Лента Мёбиуса
Про эту фигуру ты мог слышать в каких-нибудь фантастических фильмах, да и то редко. Это простейшая неориентируемая поверхность, являющаяся односторонней и непрерывной в трёхмерном пространстве. Лучше увидеть ленту Мёбиуса своими глазами, чтобы понять, что это такое. Если ты хочешь пошутить над человеком, то просто попроси его развернуть ленту Мёбиуса так, чтобы она не изгибалась. Заранее скажем, что сделать это невозможно.
7. «Рыбий пузырь»
Эта фигура больше известна как Vesica piscis, и она образована пересечением двух кругов с одинаковым радиусом, наложенных так, что центр одного лежит на окружности другого.
Где ты мог видеть такую фигуру? К примеру, в эмблеме Audi или Олимпийских игр. Также «рыбий пузырь» можно встретить в средневековой архитектуре в орнаментах и мозаиках.
8. Лемниската
Не зря лемниската идет у нас под восьмым номером, ведь своим видом она напоминает именно эту цифру, а также символ бесконечности. Эта плоская алгебраическая кривая может иметь несколько фиксированных фокусов, и от количества точек будет зависеть её конечная форма.
Почему так важно быть образованным



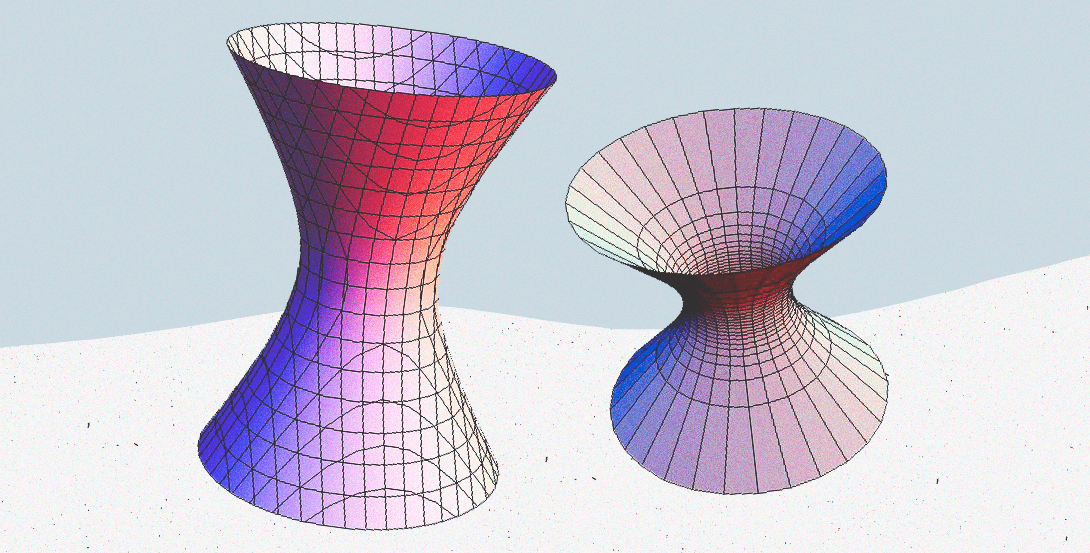


Комментарии
(0)